Lecture 2

Undirected Graphs §

$$\begin{array}{rl}G& =(V,E)\\ V& =\text{set of vertices}\\ V& =\{1,...,n\},n=|V|\\ E& =\text{set of edges}=\text{unordered pairs}\\ E& =\{(a,b),(b,c),(c,d)...\}\end{array}$$

Number of edges: $m\le \frac{n(n-1)}{2}$

Directed Graphs §

$$\begin{array}{rl}\vec{G}& =(V,\vec{E})\\ V& =\text{set of vertices}\\ V& =\{1,...,n\},n=|V|\\ E& =\text{set of edges}=\text{vectors}\\ E& =\{\overrightarrow{ab},\overrightarrow{bc},\overrightarrow{cd}...\}\end{array}$$

Number of edges: $m\le n(n-1)$

Terminology / Misc. On Graphs §

In CMPSC 130A we will only be working with simple graphs so they will not contain the following properties.

No self-loops - $(a,a)\overrightarrow{aa}$ No multi-edges $\le 1$ edge between each pair, directed $\overrightarrow{vw}\&\overrightarrow{wv}$

A cleave is a graph with every edge connected. A set is a graph with no edges. Cleaves and sets are complementary.

Adjacency Matrix §

Definition: If

$$A(i,j)=\{\begin{array}{l}1\text{ if }(i,j)\in E\\ 0\text{ if }(i,j)\notin E\end{array}$$

Undirected: $A(i,j)=A(j,i)$

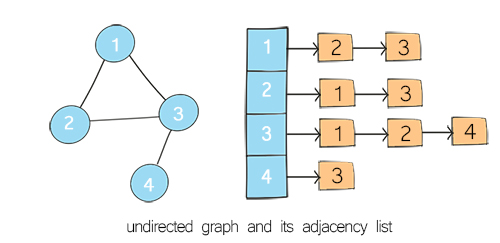
Adjacency List §

Array of linked lists.

You will number the vertices 1-n, $V=\{1,2,...,n\}$. Every vertex will have a linked list of the edges that it contains.

$A[i]$ has linked list regardless of vertex $A[i]$ has list of i’s regardless of arbitrary order.

Storage space will ALWAYS be $n\cdot m$ (number of vertices times number of edges)

Advantages:

• easy / fast to check if $(i,j)\in E$
• fast to find all neighbors of a specific vertex

Disadvantage:

• $O(n^2)$ space even if $m=O(n)$
• to check all neighbors of a vertex $i$, takes $O(n)$ time.
• to check if $(i,j)\in E$ it is $O(n)$ time

Exploring Graphs §

Ways to traverse graphs.

DFS (Depth First Search) §

Properties:

• like a maze
• explore until stuck & then backtrack
• use stack = LIFO = last in first out

Use Case: connectivity of graphs

Example 1:

DFS(G):
	Input G in adj list representation
	For all v in V, visited (v) = FALSE
	for all v in V if not visited(v) 
		then explore(v)

Explore(z): "finds all vertices reachable for z"
Visited(z) = TRUE
// (z,w) is an edge
for all (z, w) in E (this step is easy in adj. list)
	if not visited(w) then explore(w)

Running time : $O(n+m)=$ linear time Why? The code above visits every vertice and checks every edge.

BFS (Breadth First Search) §

Properties:

• check every layer as you explore
• use queue = FIFO

Use Case: distances between vertices of graphs

Connectivity in Undirected Graphs §

Two vertices a & b are connected if there is a path $a\to b$ (or $b\to a$)
Connected Component = maximal set of connected vertices
G is a connected graph if there is 1 connected component

Example: A tree is a minimal connected graph.

How to find connected components of undirected G?

1. Choose arbitrary unvisited vertex v
2. Find v’s connected component: Run Explore(v) to find all vertices reachable from v.
3. Repeat until all vertices reachable vs visitor.

DFS-cc(G):
	cc = 0 // counter
	For all v in V, visited(v) = FALSE
	for all v in V
		If not visited(v) then:
			cc++
			Explore(v)

Explore(v):
	Visited(v) = TRUE
	ccnum(v) = cc // array, connected component numbers of vertices
	for each (v, w) in E
		if w is not visited then
			Explore(w)

Runtime: O(n + m) time to find components of undirected Graph