Lecture 8

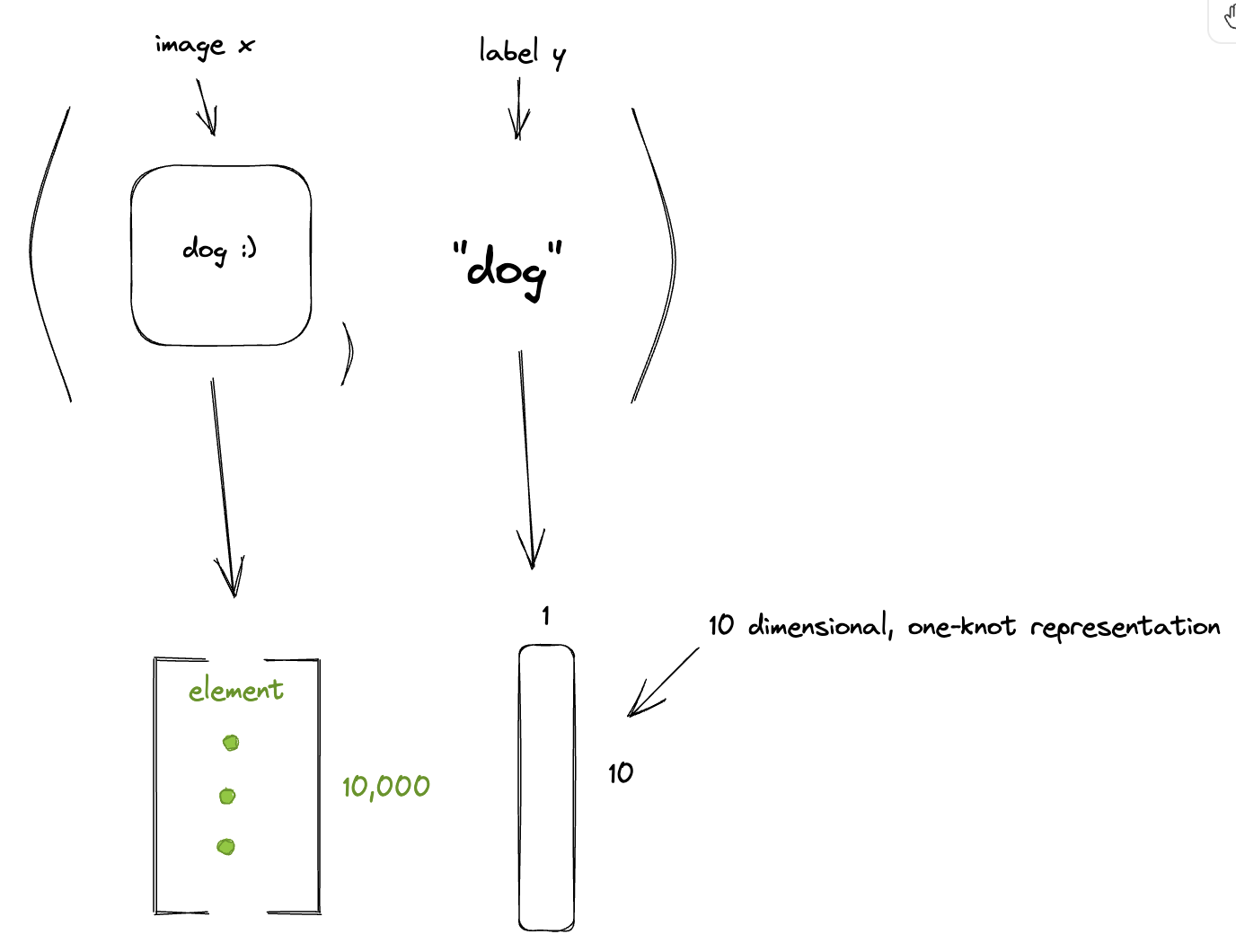
10-Class Classification §

• You are given many instances
  • Ex: You are given many pairs, images of animals and their names
  • An example could be a picture of a dog and the label “dog”
  • $x^1$ will be the image of the dog, $y^1$ will be the key “dog”
  • If there are 10 classes (10 animals), you can represent them in a 10 dimensional vector

Equation:

$$\begin{array}{r}f(\cdot )=W{x}^i\end{array}$$

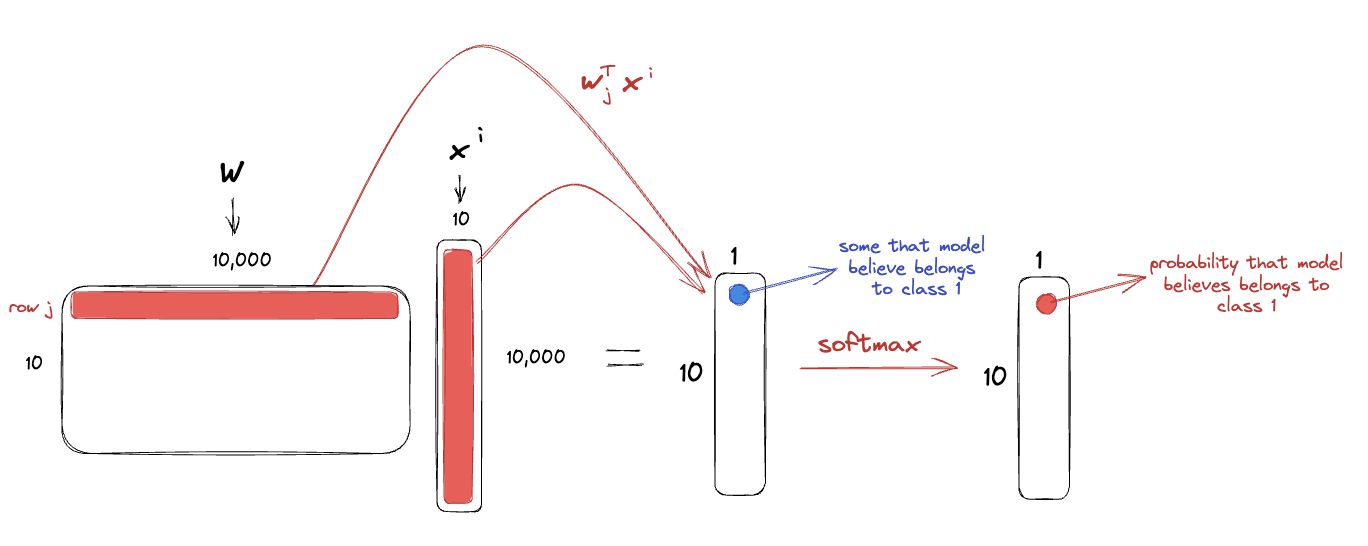
Goal: Let’s say you input $x_i$, you want $y_i$’s probability to be the highest

After the Softmax function, the $j$th element after the Softmax:

$$\frac{exp[w_j^T{x}^{(i)}]}{{\sum }_{t}exp[w_j^T{x}^{(i)}]}$$

Given $j=y^{(i)}$, we want to maximize the value above. This is to maximize the probability as the Softmax function returns the probability:

$$\max \frac{exp[w_{y^{(i)}}^T{x}^{(i)}]}{{\sum }_{t}exp[w_{y^{(i)}}^T{x}^{(i)}]}$$

This is equivalent to:

$$\min -\frac{exp[w_{y^{(i)}}^T{x}^{(i)}]}{{\sum }_{t}exp[w_{y^{(i)}}^T{x}^{(i)}]}$$

What is your input? It’s your entire weight matrix, you want to minimize the incorrect rows while maximizing the correct row.

Therefore we have to find how:

$$\begin{array}{rlr}& W_1^T& \text{update?}\\ & W_2^T& \text{update?}\\ .& & \\ .& & \\ .& & \\ & W_{y^{(i)}}& \text{update?}\\ & W_{10}& \text{update?}\end{array}$$

Claim: You can only update $W_{y^{(i)}}$ specially, this is because the rest all appear in the denominator. Only $W_{y^{(i)}}$ appears specially in the numerator and denominator and must be updated specially. Proof:

$$\begin{array}{rl}& \min -\frac{exp[w_{y^{(i)}}^T{x}^{(i)}]}{{\sum }_{t}exp[w_{y^{(i)}}^T{x}^{(i)}]}\equiv \min -\log \frac{exp[w_{y^{(i)}}^T{x}^{(i)}]}{{\sum }_{t}exp[w_{y^{(i)}}^T{x}^{(i)}]}\\ & \min -\log [exp[w_{y^{(i)}}^T{x}^{(i)}]]+\log [\sum _{t}exp[w_{y^{(i)}}^T{x}^{(i)}]]\\ & =\min -w_{y^{(i)}}^T{x}^{(i)}+\log [\sum _{t}exp[w_{y^{(i)}}^T{x}^{(i)}]]\end{array}$$

Now if we were to take the gradient with respect to some $W_1^T$ where $W_1^T$ does not correspond to $y^{(i)}$:

$$\frac{\partial }{\partial W_1^T}(\cdot )=\frac{1}{{\sum }_{t}exp[w_{y^{(i)}}^T{x}^{(i)}]}\cdot exp[W_1^T{x}^{(i)}]\cdot x^{(i)}$$

Note: Remember chain rule. Notice that this gradient would be the same for each and every $W_j^T$ where $j\ne y^{(i)}$. This is why you can have a piecewise function where you only need to take two unique gradients, $W_j^T$ where $j\ne y^{(i)}$ and where $j=y^{(i)}$.

What about SGD with multiple examples?

Place gradients as rows in $V$