Lecture 11

Multi-Layer Neural Networks §

$$h_2=\text{Softmax}(W_{2}g(W_{1}x+b_1)+b_2)$$

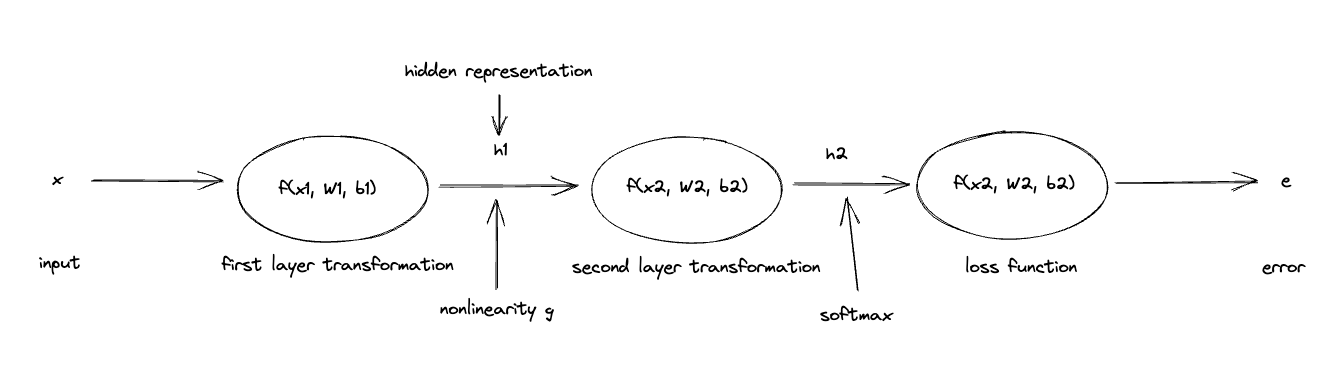
To train the network, we need to find the gradient of the error w.r.t the parameters (there are 4 in this example) of each layer, e.g. $\frac{\partial e}{\partial W_1},\frac{\partial e}{\partial W_2}$ etc.

How do you calculate the gradients of each variable? Doing it by hand is extremely tedious, what happens if you want to change your model? Backpropagation is the solution.

Backpropagation §

The key idea of backpropagation is to use chain rule on a computational graph.

Example §

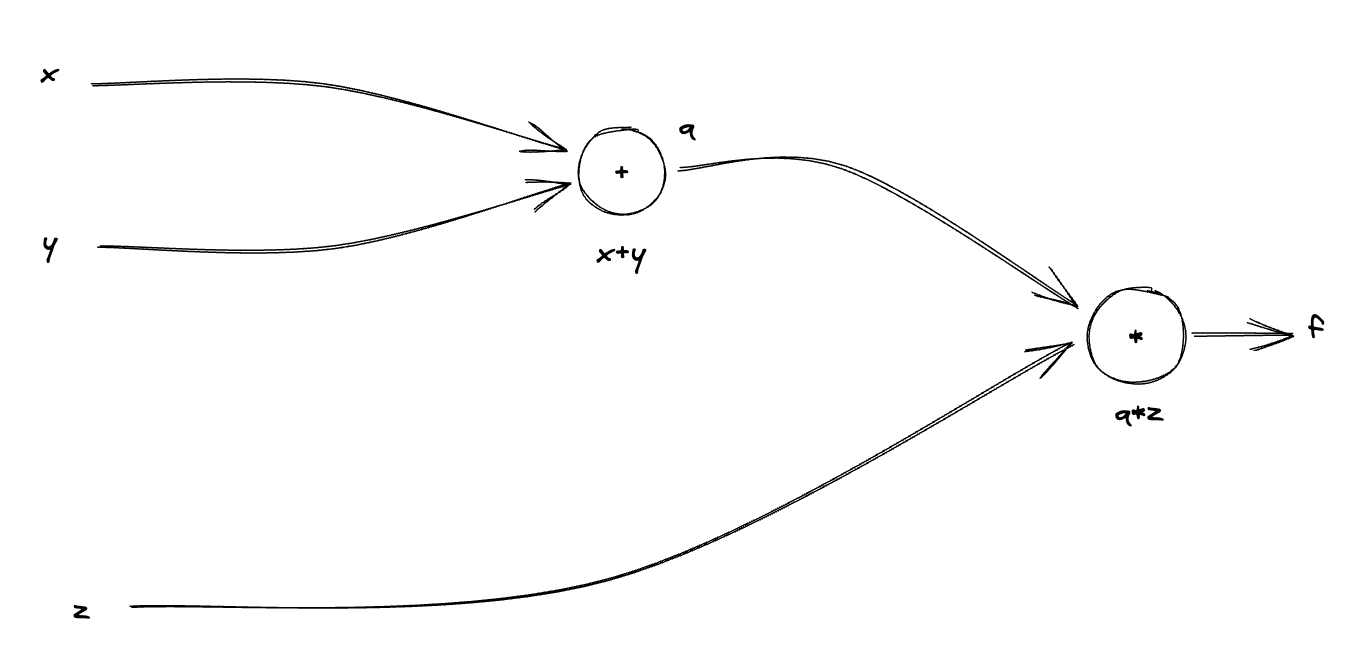
Given: $f(x,y,z)=(x+y)z\text{ where }x,y,z\in \mathbb{R}$ We know that:

$$\begin{array}{rl}\frac{\partial f}{\partial x}& =z\\ \frac{\partial f}{\partial y}& =z\\ \frac{\partial f}{\partial z}& =x+y\end{array}$$

Here is the computational graph:

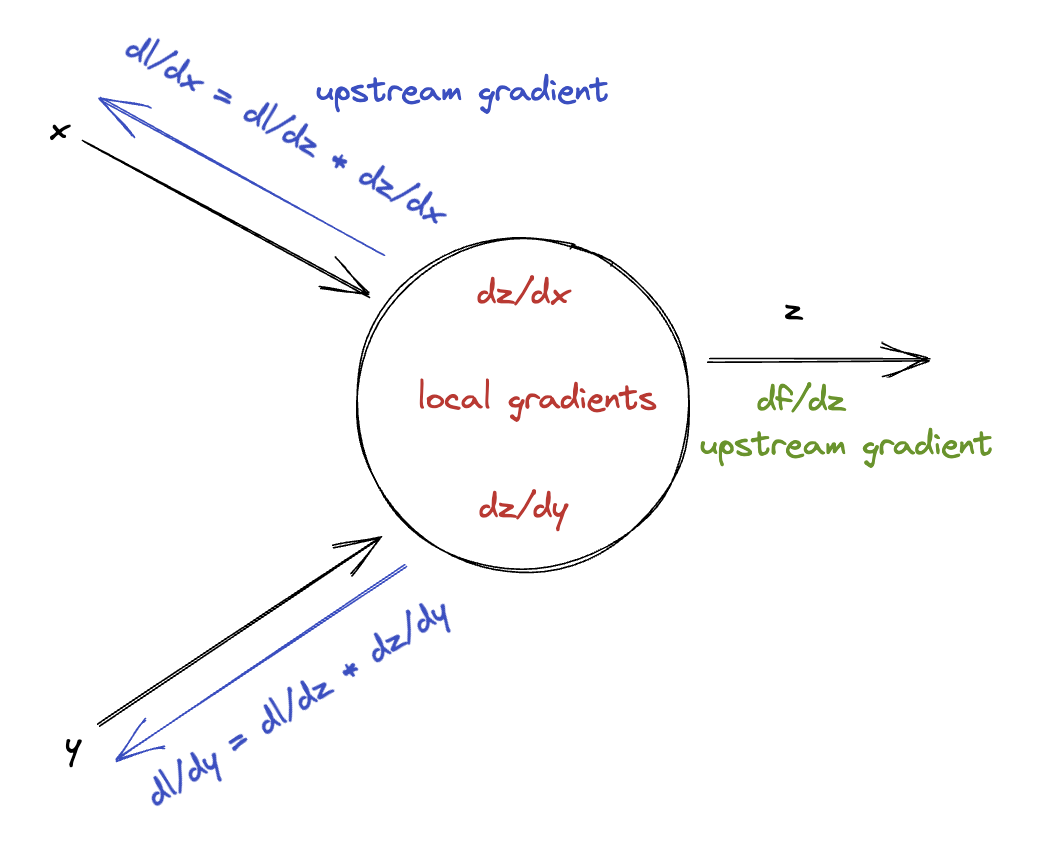
The way back propagation works is by working from the final layer and propagating backward by taking the upstream gradient and the local gradients and propagating backwards.

You can picture a node in the computational graph like this.

Midterm 1 Review §

Three Portions:

1. True or False, 6 Questions, 18 Points
2. Multiple Choice, 8 Questions, 32 Points
3. Major Questions, 3 Questions (Derivations / Short Answers etc.), 50 Points

Topics: XOR Problem (MUST REVIEW)

Multiclass Derivation

• Shape of each parameters
• Anything in Lecture 8 is fair game

Broadcasting in Python

Simple matrix and probability

• Understand the shape of the Matrix
• Shape of gradient

Probability (Bayes’ Rule)

Linear Regression

• Analytical Solution
• Be able to transform between $||XW-y|{|}_2^2$ to $||xw+b-y|{|}_2^2$ and explain how
• Know how to DERIVE analytical solution

Ridge Regression

• $\lambda ||w|{|}_2^2$
• Know how to derive the analytical solution
• Are there any constraints to lambda (lambda must be positive, why? hint: think about minimizing meaning THERE WILL BE NO MINIMUM IF LAMBDA IS NEGATIVE)

Stochastic Gradient Descent / Gradient Descent / Optimization / Vector Calculus

• What is the definition of the gradient
  • Remember, the gradient is always in the direction of the function increasing
  • That’s how we minimize loss, we subtract the gradient
• How does learning rate affect gradient descent
  • Too big? Overshooting, wild oscillation
  • Too small? long time to converge
  • Extremely big/small? flat

Difference between GD and SGD

• Gradient Descent will be smoother vs. SGD
• Initializations
• If the answer is convex, in the perfect case you will find the minimum

Logistic Regression

• Analytical VS Gradient Descent (gradient descent is right)
• Sigmoid($\cdot$) $p(y=1|x)$
• Decision rule for logistic regression
• Sigmoid($\cdot$) vs softmax($\cdot$) They are equivalent in the 2 class scenario

Multi-class

• In class derivative
• How will w update when given a certain input
• Softmax - There are special characteristics of the softmax function. If you can calculate the Softmax($v$) where $v$ is a vector. Will the answer be the same as if you added a constant to every element of the Softmax. It will be the same. But if you multiply it will not be the same. From a numerical stability standpoint you want to subtract the greatest from every element of the softmax.

Python Coding

• Finding bugs
• Broadcasting shapes

FNN

• Nonlinearities AKA Activation Functions, why you need them
• Best choice is ReLu
• $g(W_{2}g(W_{1}x+b_1)+b_2)$
  • Note that if x is of dimension d, then W must be of dimension $z\times d$. Note that it has to be consistent with $W_2$
• Overfitting vs Underfitting phenomenon

$$\begin{array}{rl}& f(w)\in \mathbb{R}\\ & \text{if w is a scalar}:\frac{\partial f}{\partial w}=\text{scalar}\\ & \text{if w is a vector}:\frac{\partial f}{\partial w}=\text{vector of same shape}\end{array}$$

Notes: There will be no coding portion on the exam, you are only expected to perform multiple choice questions on coding. TWO QUESTIONS IN CODING