Lecture 7

Minimum Spanning Tree (MST) §

For a graph $G=(V,E)$, for $S\subset E$, $H(V,S)$ is a subgraph of $G$ (Subset of $S$ edges).

A tree $T\subset E$ is a subgraph which is connected & acyclic.

A forest is a subgraph which is acyclic. (A tree is a type of forest)

MST = minimum spanning tree

Find a subgraph of minimum weight which is a tree (connected & acyclic)

Given a graph $G=(V,E)$ with $\omega (e)>0$ for $e\in E$ for $S\subset E$:

$$\text{Let }\omega (s)={\Sigma }_{e\in S}\omega (e)$$

MST problem: Given $G(V,E)$ with $\omega (e)>0$ for $e\in E$, find $S\subset E$ which is connected & minimizes $\omega (s)$. (We assume G is connected)

Example:

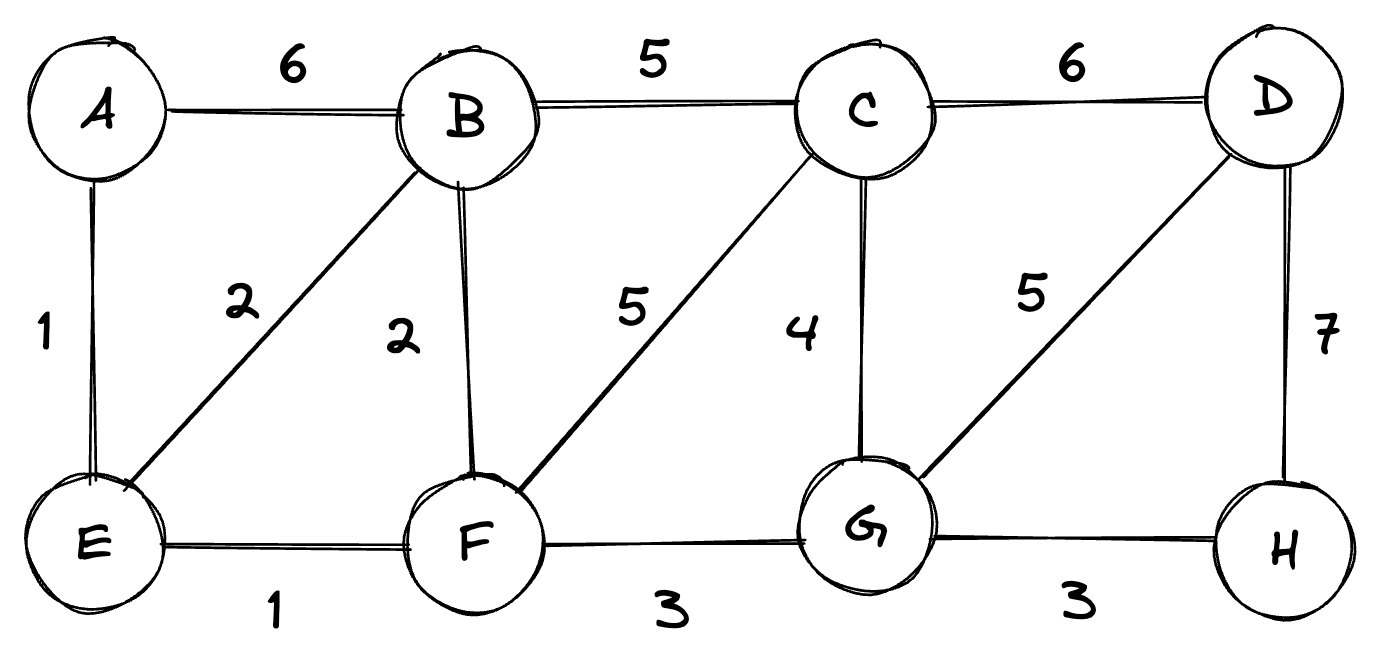
Weight of this graph is: $1+1+2+3+3+4+5=19$ ($AE+EF+BF+FG+CG+DG+GH$)

There are two possible MST’s, you could either use BF or BE.

Basic graph theory:

1. Tree on n vertices has $n-1$ edges
2. Any connected graph with exactly $n-1$ edges is a tree.
3. In a tree there is exactly one path between every pair of vertices.

Prim’s Algorithm §

T = partially explored set of vertices (arbitrary start) X = MST on T

for z not in T: cost(z) = min edge weight between z and T

next explored vertex: z not in X with min cost(z)

$O((n+m)(\log n))=O(m\log (n))$ ($m\ge n-1$)

Prim(G,w):
input: undirected G = (V,E) with w(e) > 0
output: MST defined  bby prev()
	for all v in V
		cost(v) = infinity
		prev(v) = NULL
	
	Choose any v in V to set to be s
	cost(s) = 0
	H = empty heap
	
	For all v in V Insert(H, v, cost(v))
	While H:
		v = Delete Min(H)
		For(V, z) in E:
			if cost(z) > w(v,z) then: 
				cost(z) = w(v,z)
				DecreaseKey(H, z, cost(z))
				prev(z) = v

Kruskal’s Algorithm §

Greedy approach $\to$ try to add edge with minimum weight.

For input $G=(V,E)$,

1. Sort E by increasing weight ($O(m\log n)$ time by merge sort)
2. Let X = $\varnothing$
3. Go through edges in increasing order of weight: for edge e = (y,z): if X $\cup$ e is acyclic then add e to X

Union-find data structure (Disjoint sets data structure):

• Maintain connected components in partial MST (v,x)
• To check if x union E is acyclic we check if y & z are connected in (v,x) Operations:
• MakeSet(x): create a new set just containing X $O(1$)
• Find(x): return name of set containing x $O(\log n$)
• Union(x,y): merge the sets containing x and y $O(\log n$)

Krushkal (G,w):
	For all z in V, MakeSet(z)
	x = emptyset
	Sort E by increasing weight
	Go through E in increasing order
		For edge e = (y,z):
			if Find(y) != Find(z) then:
				X = X union e
				Union(y,z)
	return x

Proof of correctness :
Cut property:
Krushkal’s — Why is it correct?
Proof of induction on |X|
Partial MST X on explored set S
Base Case: X is empty, S = {s},
Assume by induction that X is a partial MST on S that means there is a MST T on G where X $\subset$ T
Let $e=(Y,z)$ be the next edge added to $X$
We need to show: There is a MST $T^{\prime }$ where $X\cup e\subset T^{\prime }$

This is implied by the following more general cut property