Lecture 3

Directed Acyclic Graph §

Acyclic: No Cycles

DFS in DAG §

DFS with a clock $\to$ preorder #, postorder

Pseudocode DFS:

DFS(G):
	input: undirected or directed graph in adj. list
	for all v in V, visited(v) = FALSE
	clock = 1 # NEW STEP COMPARED TO UNDIRECTED GRAPH
	for all v in V if not visited(v) then Explore(v)

Explore(w):
	visited(w) = TRUE
	preorder(w) = clock
	clock++
	for every edge out in E:
		if not visited(z) then Explore(z)
	post(w) = clock
	clock++

Example Run:

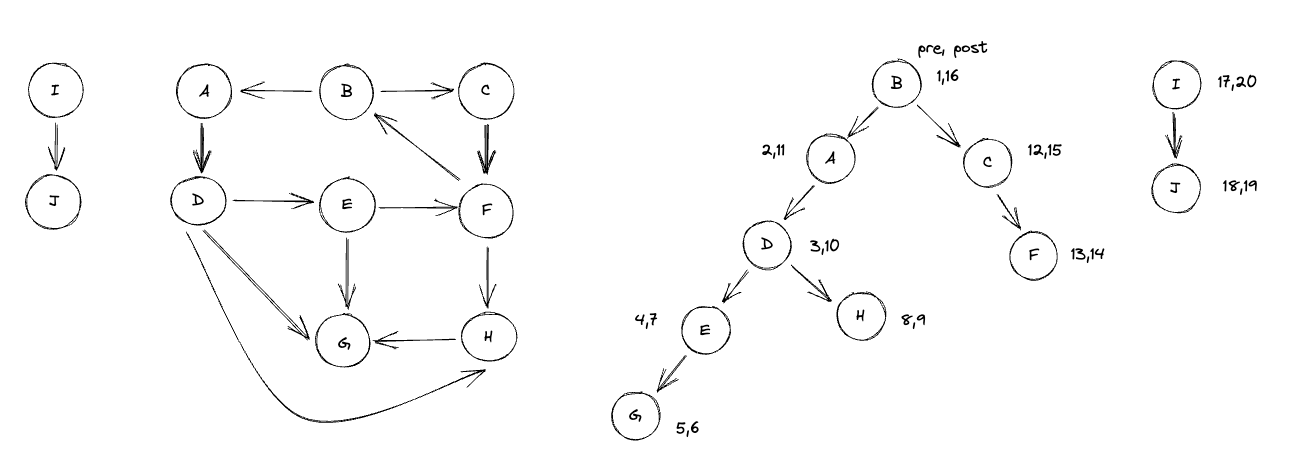
Classification of Edges §

Given Edge $v\to w$

Forward

• post(v) > post(w)
• Ex: D $\to$ G
• Pre(D) < Pre(G) < Post(G) < post(D)

Back:

• post(v) > post(w)
• Ex: F $\to$ B, J $\to$ I
• pre(B) < pre(F) < post(F) < post(B)

Cross:

• post(w) > post(v)
• Ex: F $\to$ H, H $\to$ G
• pre(H) < post(H) < pre(F) < post(F)

Key Claim: §

Directed $\vec{G}$ has a cycle IF AND ONLY IF its DFS tree has a back edge.
i.e If there are no cycles in a graph, then there are NO back edges in DFS tree.

Proof:
Suppose graph $\vec{G}$ has $\ge$ 1 cycle, call it C = $v_0\to v_1\to v_2\to ...\to v_0$
Consider DFS, some vertex in C is visited first, call it $v_i$. $v_i$’s subtree in DFS tree will equal every vertex reachable from $v_i$ and is not yet visited.
Suppose DFS tree has back edge $v\to w$.

How to detect if a graph is a DAG or not?
Run DFS and keep every pre / post #
Check every edge v $\to$ w, see if back edge post(v) < post(w) then report a cycle.

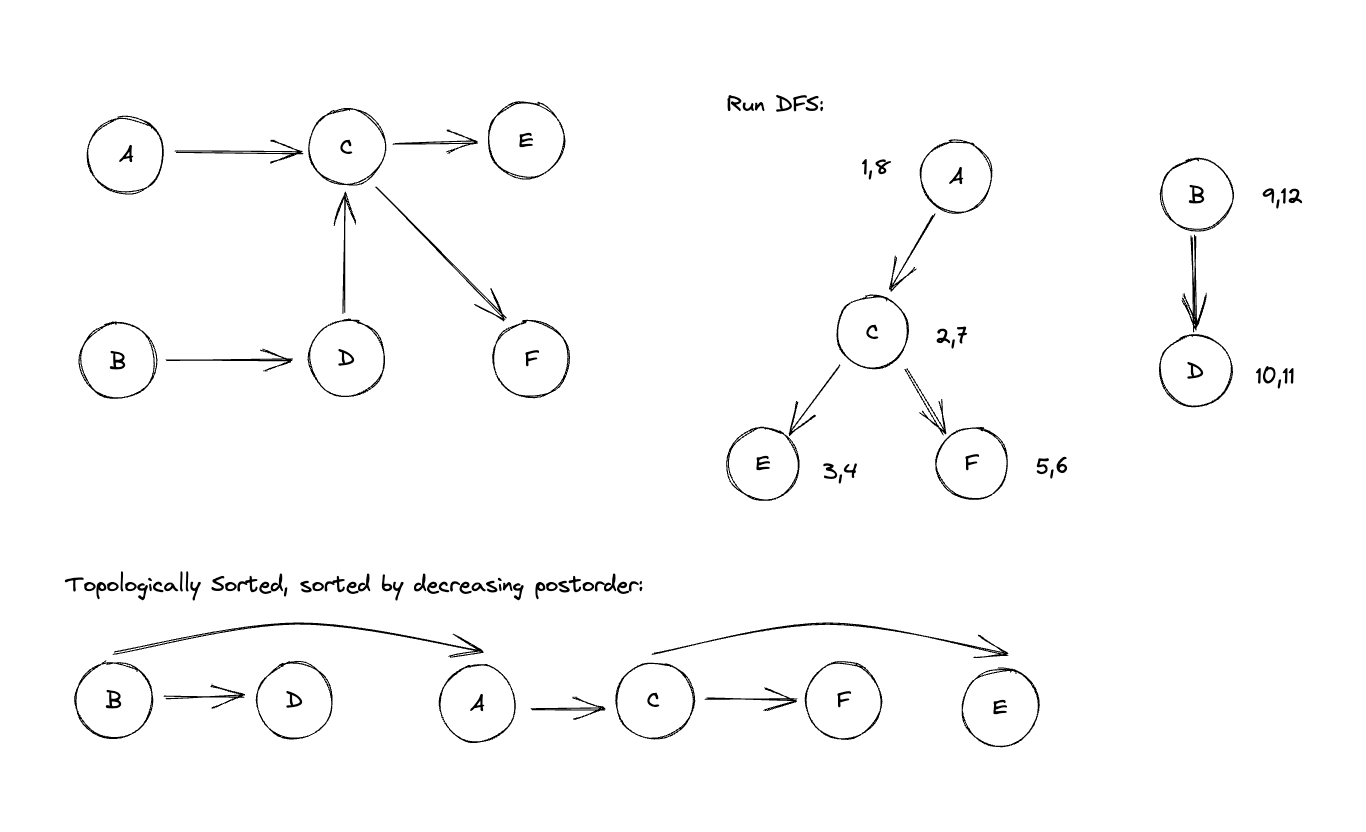
Topologically sort a DAG §

Order vertices so all edges go left(earlier) to right (later).

Run DFS & order by post order #. Takes O(n + m) time.

Classification of Vertices §

Source Vertex

• An vertex with no incoming edges
• In a DAG, there is guaranteed to have at least one source vertex
• Note that in a topologically sorted DAG, the leftmost vertex will be a source vertex.

Sink Vertex

• A vertex with no outgoing edges.
• In a DAG, there is guaranteed to have at least one sink vertex
• Note that in a topologically sorted DAG, the rightmost vertex will be a source vertex.

Arbitrary Directed Graph §

Directed graph with arbitrary edges, cycles are allowed.

Strongly Connected §

v & w are strongly connected if v $\to$ w & w $\to$ v.
Strongly Connected Components (SCC): Maximal set of strongly connected pairs Goal: find SCC’s of arbitrary directed graph