Lecture 4

General Directed Graphs §

Vertices a & b are strongly connected if path $a\to b$ and $b\to a$.

SCC: Strongly Connected Component = maximal set of strongly connected vertices.

Metagraph on SCC’s: Vertex for each SCC. Edge $S\to S^{\prime }$ if some $a\in S$ & $b\in S^{\prime }$ has edge $\overrightarrow{ab}$.

Example:

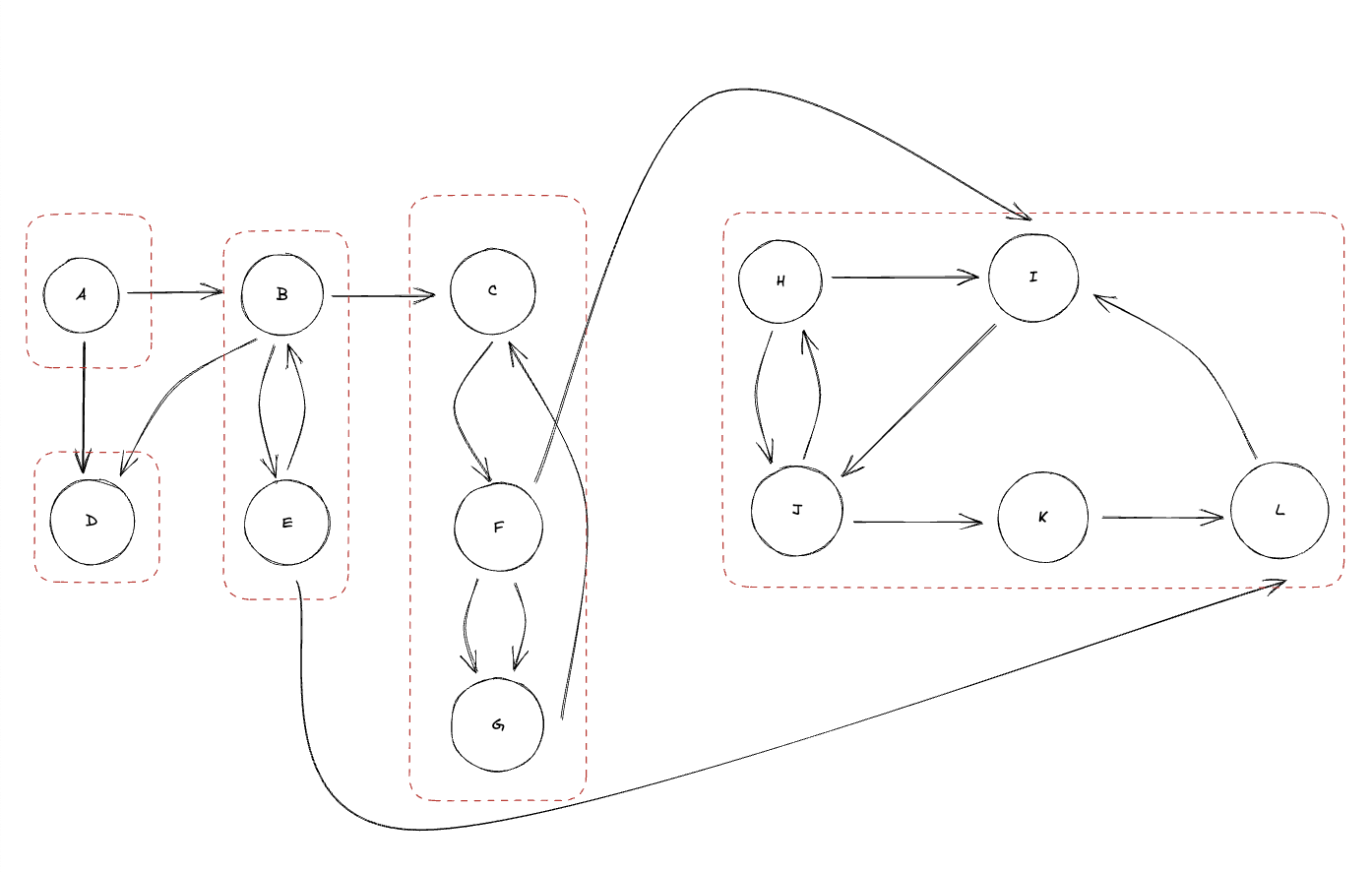
Within Red boxes are SCC’s.

Metagraph on SCC’s: 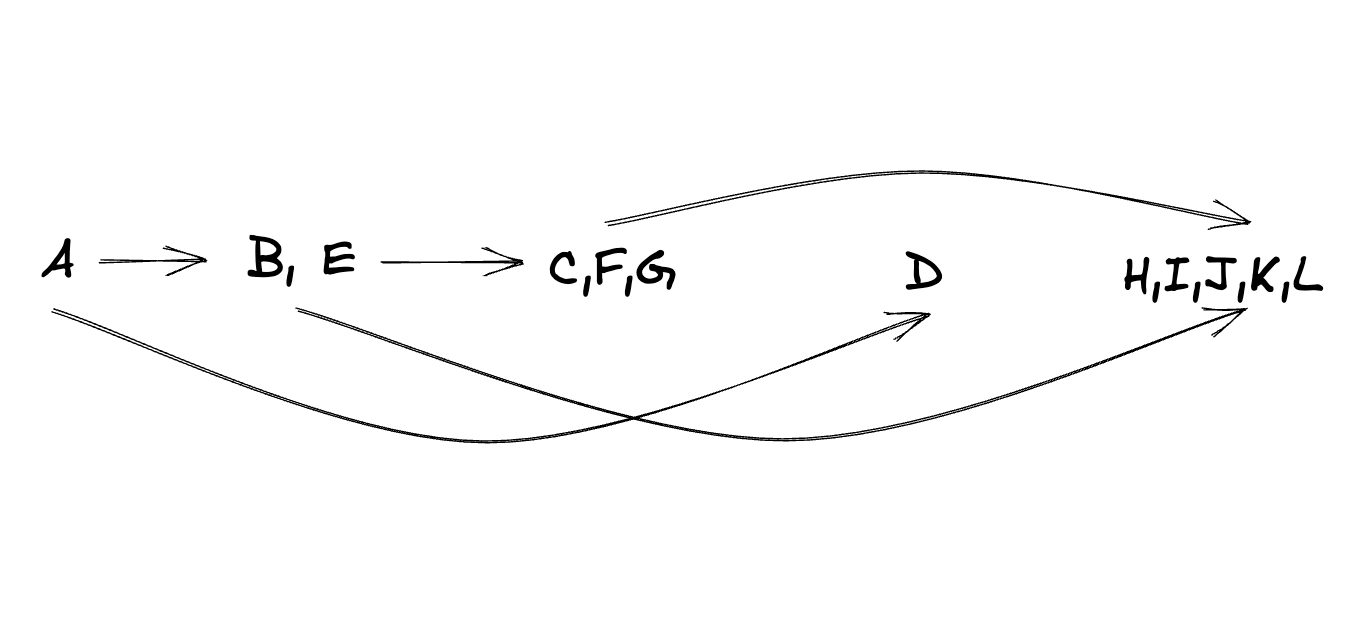This metagraph is a DAG.

Key: Every directed graph is a DAG on its SCC’s. Why? What if there is a cycle in SCC graph?

FALSE Conjecture: In a general directed graph vertex with lowest post # is in a sink SCC

Lemma: In a directed graph, the vertex with the highest post # lies in a source SCC.

Source $SC{C}^S$ is opposite of sink $SC{C}^{S^{\prime }}$.
The reverse of $\vec{G}=(V,\vec{E})$: ${\vec{G}}^R=(V,{\vec{E}}^R)$ (FLIP EVERY EDGE)
Note that the SCC’s in $\vec{G}$ will be the same as the SCC’s in ${\vec{G}}^R$
However, the DAG on SCC’s is flipped.
Source $SC{C}^S$ in $\vec{G}$ = equal to sink $SC{C}^S$ in ${\vec{G}}^R$
Sink $SC{C}^{S^{\prime }}$ in $\vec{G}$ = Source $SC{C}^{S^{\prime }}$ in ${\vec{G}}^R$

Final SCC Algorithm §

1. Given $\vec{G}=(V,\vec{E})$, construct ${\vec{G}}^R=(V,{\vec{E}}^R)$
2. Run DFS on $\vec{G}$
3. Sort V by decreasing postorder number from step 2
4. Take unvisited vertex $v\ast$ with highest postorder number
5. Run Explore($v\ast$) and label as a new SCC
6. Repeat until all vertices are visited

For input G = (V, E)

Construct the Reversed Graph GR
Run DFS on GR and keep pre and post order number
Order V by decreasing post order number
run undirected connected components algorithm on G to find SCC's in G

DFS-cc(G):
	For all vertices in V, set visited(v) = False
	cc = 0
	For all v in Vertices(Ordered by decreasing post order number)
		If not visited(v)
			then cc++
			Explore(v)

Explore(z):
	visited(z) = T
	sccnum(z) = scc
	for all edges in e:
		if not visited(w) then explore(w)

Lemma Proof §

Lemma: In a directed graph, the vertex with the highest post # lies in a source SCC. Proof: Claim: If S & S’ are SCC’s & there is edge $a\in S$, $b\in S^{\prime }$, there is an edge $\overrightarrow{ab}\in \vec{E}$

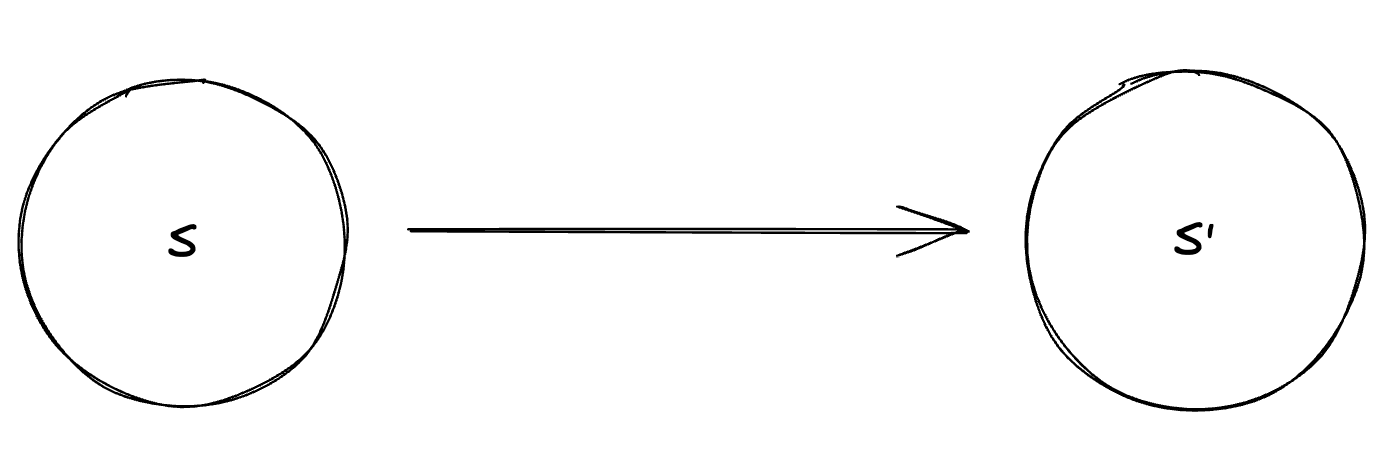
The max post # in S > than the max post # in S’

Only the claim has to be proved to prove the Lemma. If the claim is true then the SCC with the vertex with the greatest post order number then is MUST be true that it is the source SCC as no other SCC’s could point to it.

Proof of claim: Run DFS, take 1st vertex in $S\cup S^{\prime }$ that’s visited, call it Z.