Lecture 5

BFS §

Input graph G(VE) in adj. list format - diercted or undirected and s in V

Output: for all v in V, dist(v) = min # of edges to go from s to v = length of shortest path

For all v in V, dist(v) = infinity
dist(s) = 0
Q = {S} (create a new queue containing only s)
While Q isn't empty
	w = deque(Q)
	for all w in E
		if the distance(z) = inifnity then:
			enqueue(Q, Z)
			dist(z) = dist(w) + 1

BFS vs DFS §

BFS uses a queue, FIFO vs. DFS which uses a stack, LIFO

Dijkstra’s §

Dijkstra’s algorithm aims to answer the question, what is the dist(v) from s = A?

for edge e, l(e) > 0
A to B to G to H (dist(A to B) = 1, dist(B to G) = 6, dist(G to H) = 1)
	l(A to B to G to H) = 8
dist(v, w) = min over all paths v to w of length P = length of shrotest v to path
	dist(A, H) = 6 = (1 + 2 + 2 + 1)

BFS: finds “distances” from s to every other vertex where G is an unweighted graph. What if weights / lengths on edges?

Dijkstra(G, l, s):
	input: graph G = (V, E), with lengths l(e) > 0 for e in E and s in V
	output: for all v in V, dist(v) = length of shrotest s to v path

Example §

Imagine you want to find the shortest path and don’t want to edit the BFS algorithm (suppose it’s a black box), you could add nodes in between corresponding to the length of the path.

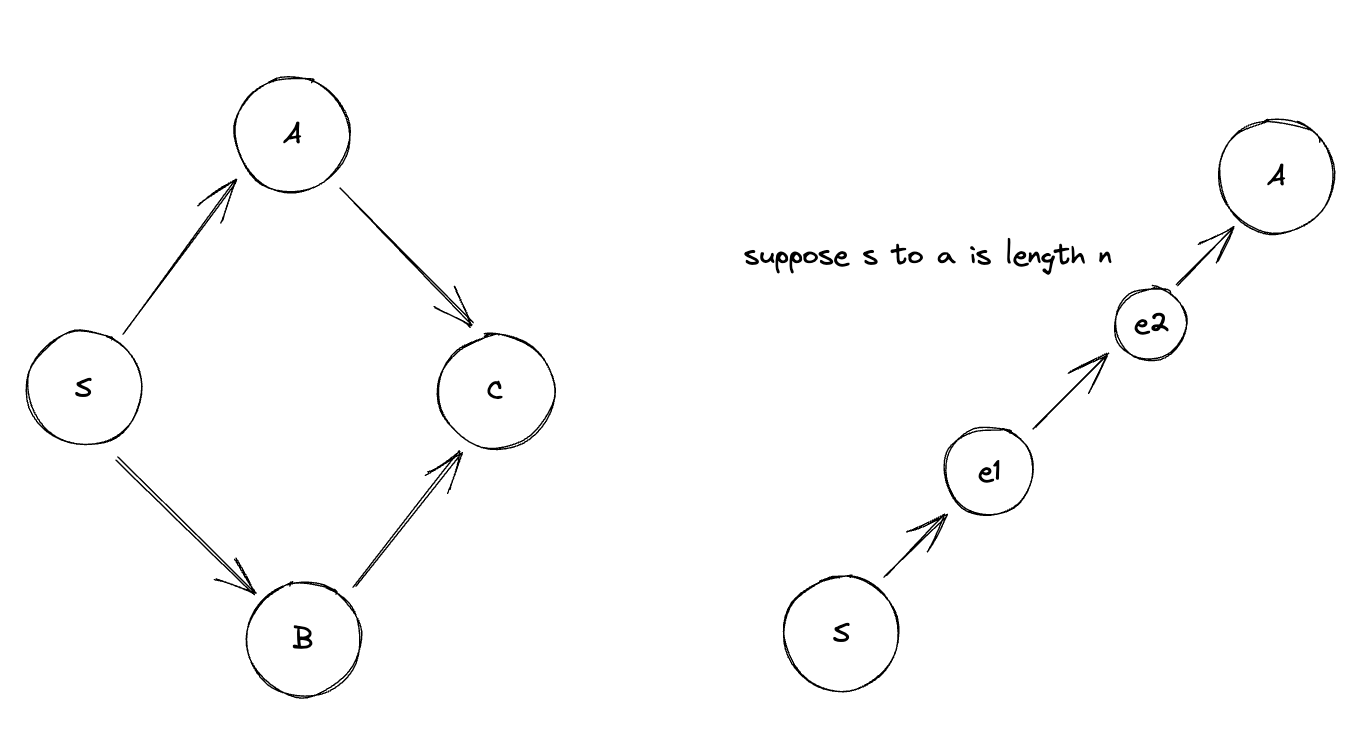
Two problems:

• Integer lengths only
• Running time $\approx$ # of vertices in G’
• What if length l(e) is HUGE, V(G’) is HUGE, or n’ is HUGE

We can solve this by using an “Alarm Clock” for each vertex in the original graph:

Run Time: $O((n+m)\log n)$

dist(v) = time for v's clock = min length path from s to v using explored vertices so far

Min heap data structure:
	heap H is a set of elements(vertices)
		each has a key dist(v)

Operations:
	Insert(H, v, dist(v)): 
		inserts a new element v onto heap V with key dist(V)
	Decrease Key(H, v, dist(v)):
		for element v in H, decrease its key to dist(v)
	Delete Min(H):
		Output the element with min key value in H and delete it from H

Dijkstra(G, l, s):
	input G = (V, E) with l(e) > 0 for all e in E and s in V
	output: for all v in V, dist(v) = length of shortest s to v path
	
	prev(v) = parent of v on shortest s to v path
	for all w in V:
		dist(w) = infinity
		prev(w) = null
	dist(s) = 0
	H = not empty
	for all v in V, Insert(H, v, dist(v))
		while H is not equal to not empty:
			w = delete min(H)
			for all w in E
				if dist(w) + l(w, z) < dist(z) then:
					dist(z) = dist(w) + l(w,z)
					prev(z) = w
					Decreasekey(H, Z, dist(z))