Lecture 9

Simple Nonlinear Prediction §

The “shallow” approach: nonlinear feature transformation (often by hand), followed by a linear classifier

Cons:

• The design of a good feature transformation can be tricky
• The number of new features

Multi-layer Neural Network §

The deep approach: stack multiple layers of linear transformations interspersed with nonlinearity

Two layer neural network:

$$\begin{array}{r}f(x)=W_2(W_{1}x+b_1)+b_2\end{array}$$

For an N layer neural network:

$$\begin{array}{r}f(x)=W_{N}g(...W_2(W_{1}x+b_1)+b_2...)+b_N\end{array}$$

Nonlinearity §

Sigmoid: $g(x)=\frac{1}{1+e^{-x}}$

• Historically very popular
• Squashes numbers to range $[0,1]$
• Saturated neurons “kill” the gradients

Sigmoid: $g(x)=\tanh (x)$

• Squashes to range $[-1,1]$
• Still kills gradients

Relu: $g(x)=\max (0,x)$

• Does not saturate (in + region)
• Very little computation
• What is the gradient when $x<0$
• MOST POPULAR

Leakey Relu: $g(x)=\max (.05x,x)$

• Neuron will not die
• In practice, use Relu on your first try.

Why We Need a Nonlinear Function §

If there is no nonlinearity, no matter how many layers you stack, you will still be modeling a linear relationship.

Proof by Example (XOR) §

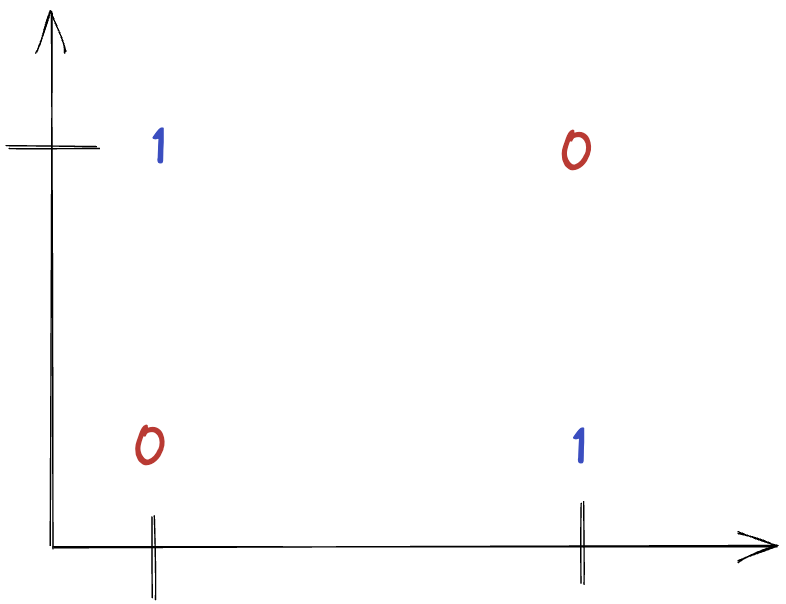
$x_1$	$x_2$	label
0	0	-1
0	1	1
1	0	1
1	1	-1

Can we find a two layer MLP to solve this problem?

$$\begin{array}{rl}& f(x)=W_2\max (W_{1}x+b_1,0)+b_2\\ & x\in {\mathbb{R}}^2,W_1\in {\mathbb{R}}^{d\times 2},W_2\in {\mathbb{R}}^{1\times d}\\ & b_1{\mathbb{R}}^d,b_2\in \mathbb{R}\end{array}$$

Let $d=2$, for the following derivations

MLP: $f(x)=W_2\max (W_{1}x+b_1,0)+b_2$ where

$$\begin{array}{rlr}{W}_1& =\left|\begin{array}{cc}2& -1\\ -1& 2\end{array}\right|,& b_1=\left|\begin{array}{c}0\\ 0\end{array}\right|\\ W_2& =(1,-1),& b_2=-1\end{array}$$

Training Neural Networks §

Steps:

• Collect / clean data and labels
• Specify model: select model class / architecture and loss function
• Train model: find the parameters of the model that minimizes the empirical loss on the training data

How to best find Hyperparameters §

Your goal is always to make a generalizable model. Not to overfit.

• For training, there are typically two losses you should monitor
  • Loss on the training data - how well the model will perform
  • Loss on the validation data - how well the model generalizes

	Simple	Complex
Low	Ok	Underfitting
Higher	Overfitting	Ok