Lecture 2

Dot Product §

Recall the definition of the dot product:

$$\begin{array}{rl}& \vec{v}=<v_1,v_2,v_3>,w=<w_1,w_2,w_3>\\ & \vec{v}\cdot \vec{w}=v_1\cdot w_1+v_1\cdot w_2+v_3\cdot w_3\end{array}$$

Properties of Dot Product §

Let $\vec{u},\vec{v},\vec{w}$ be three vectors.

Valid Properties §

Distribution: $\vec{u}\cdot (\vec{v}+\vec{w})=\vec{u}\cdot \vec{v}+\vec{u}\cdot \vec{w}$
Commutativity: $\vec{u}\cdot \vec{v}=\vec{v}\cdot \vec{u}$

Invalid Properties §

Associativity: For $a,b,c\in \mathbb{R}$ we have $a\cdot (b\cdot c)=(a\cdot b)\cdot c$

Although true for real numbers, associativity does not hold for dot products $(\vec{u}\cdot \vec{v})\cdot \vec{w}\ne \vec{u}\cdot (\vec{v}\cdot \vec{u})$ Example:

$$\begin{array}{rl}& \vec{u}=<1,0>,\vec{v}=<1,1>,\vec{w}<0,1>\\ & \vec{u}\cdot \vec{v}=1,(\vec{u}\cdot \vec{v})\cdot \vec{w}=1\cdot \vec{w}=\vec{w}=<0,1>\\ & \vec{v}\cdot \vec{w}=1,\vec{u}\cdot (\vec{v}\cdot \vec{w})=\vec{u}\cdot 1=\vec{w}=<1,0>\end{array}$$

Geometric Properties of the Dot Product §

Let $\vec{v},\vec{w}$ be vectors in ${\mathbb{R}}^2$ (this also works in ${\mathbb{R}}^3$)

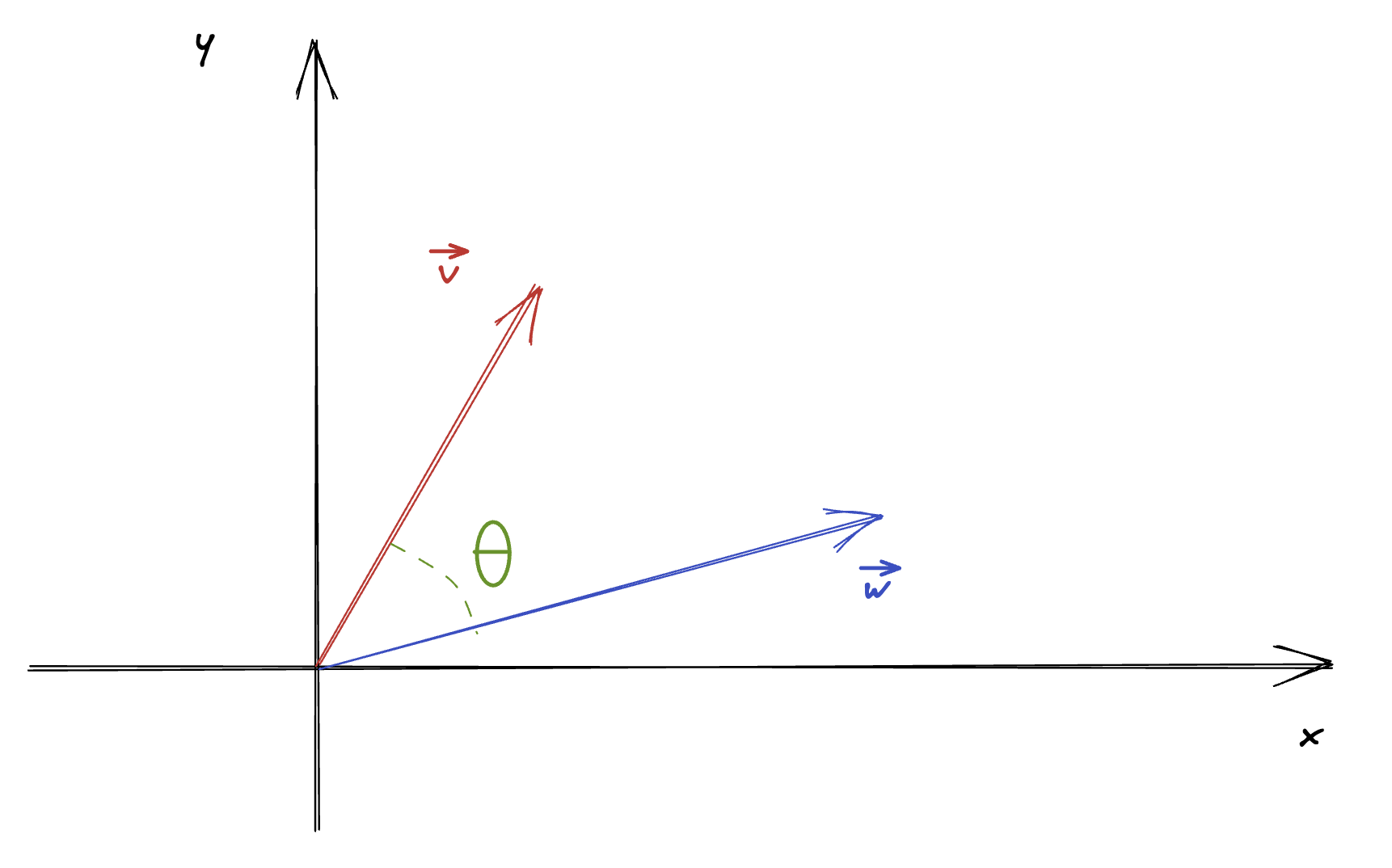
Observations: The angle between the two vectors is between 0 and x.

• When $\theta =0$, we say that $\vec{v}$ and $\vec{w}$ are parallel vectors.
  • $\vec{v}\cdot \vec{w}=||\vec{v}||\cdot ||\vec{w}||$.
• When $\theta =\pi /2$, we say that $\vec{v}$ and $\vec{w}$ are orthogonal or perpendicular to each other.
  • $\vec{v}\cdot \vec{w}=||\vec{v}||\cdot ||\vec{w}||\cdot \cos \frac{\pi }{2}=0$
• $\theta =\pi$, we say that $\vec{v}$ and $\vec{w}$ are in opposite directions
  • $\vec{v}\cdot \vec{w}=||\vec{v}||\cdot ||\vec{w}||\cdot \cos \pi =-||\vec{v}||\cdot ||\vec{w}||$

Scalar §

Recall:

$$\begin{gathered} \vec{v}=<v_1,v_2,v_3>,\lambda \in \mathbb{R} \\ \lambda \cdot \vec{v}=<\lambda v_1,\lambda v_2,\lambda v_3> \end{gathered}$$

Scalar Properties §

Let $\vec{v},\vec{w}$ be vectors and $c\in \mathbb{R}$

$$(c\cdot \vec{v})\cdot \vec{w}=c\cdot (\vec{v}\cdot \vec{w})$$

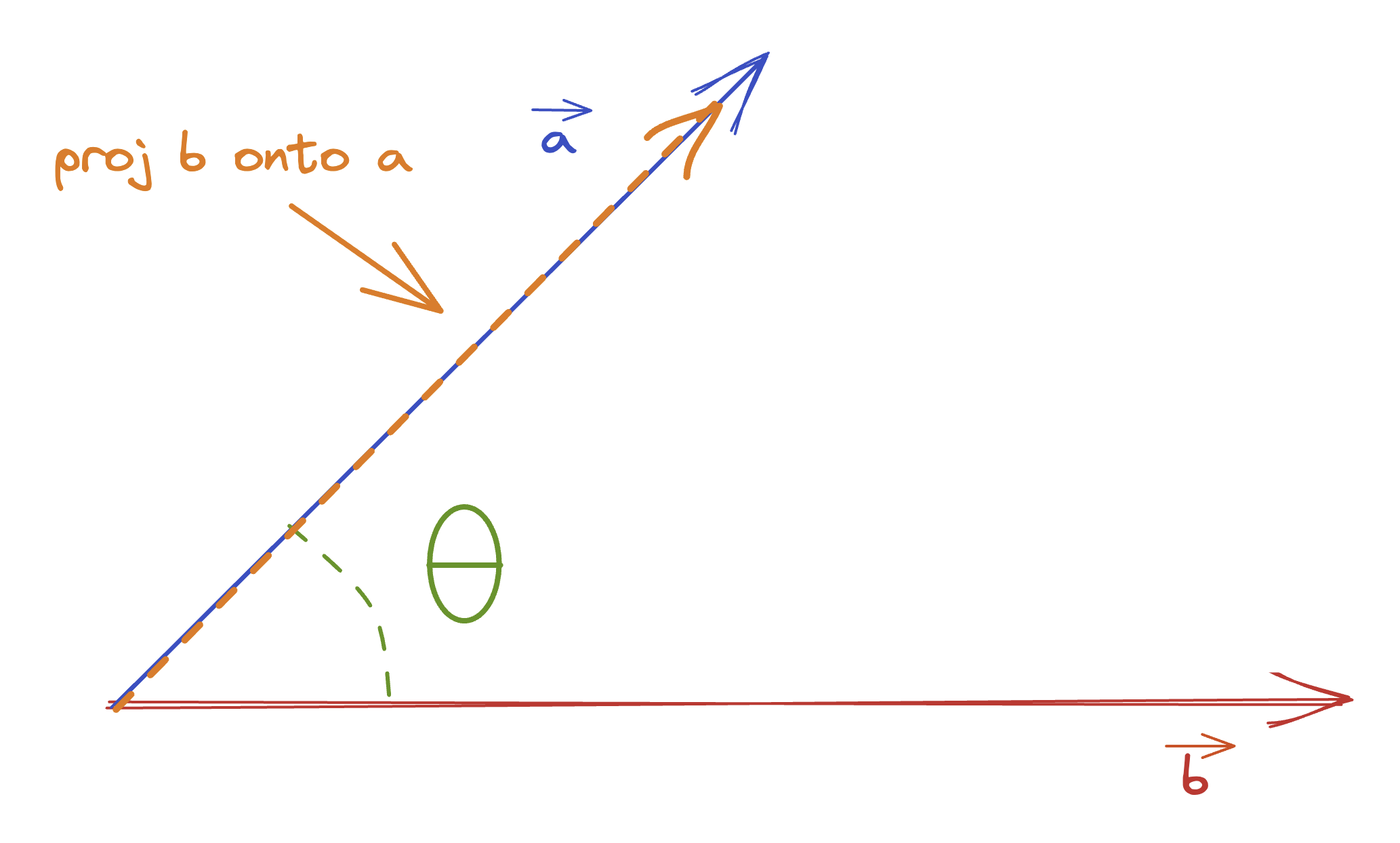
Projection §

Let $\vec{a}$ and $\vec{b}$ be two vectors. The projection of $\vec{b}$ onto $\vec{a}$ is defined as:

$$pro{j}_{\vec{a}}\vec{b}=\frac{\vec{a}\cdot \vec{b}}{||\vec{a}|{|}^2}\cdot \vec{a}$$

Recall the geometric property of dot products:

$$\vec{a}\cdot \vec{b}=||\vec{a}||\cdot ||\vec{b}||\cdot \cos \theta$$

$$\begin{array}{rl}pro{j}_{\vec{a}}\vec{b}& =\frac{\vec{a}\cdot \vec{b}}{||\vec{a}|{|}^2}\cdot \vec{a}\\ & =\frac{||\vec{a}||\cdot ||\vec{b}||\cdot \cos \theta }{||\vec{a}|{|}^2}\cdot \vec{a}\\ & =(||b||\cdot \cos \theta )\cdot (\frac{\vec{a}}{||\vec{a}||})\end{array}$$

Here is an image to help with your conceptualization:

Why Project? §

Think about in physics where sometimes you want only a vertical or horizontal component of a force. Projection works much the same, for some equations we may only want the component in the same direction as a vector.

Cross Product §

The cross product in ${\mathbb{R}}^3$:

$$\begin{array}{rl}\vec{v}& =<v_1,v_2,v_3>=v_1\cdot \vec{i}+v_2\cdot \vec{j}+v_3\cdot \vec{k}\\ \vec{w}& =<w_1,w_2,w_3>=w_1\cdot \vec{i}+w_2\cdot \vec{j}+w_3\cdot \vec{k}\\ & \\ \vec{v}\times \vec{w}& =\left|\begin{array}{ccc}\vec{i}& \vec{j}& \vec{k}\\ v_1& v_2& v_3\\ w_1& w_2& w_3\end{array}\right|=\left|\begin{array}{cc}{v}_2& v_3\\ w_2& w_3\end{array}\right|\cdot \vec{i}-\left|\begin{array}{cc}{v}_1& v_3\\ w_1& w_3\end{array}\right|\cdot \vec{j}+\left|\begin{array}{cc}{v}_1& v_2\\ w_1& w_2\end{array}\right|\cdot \vec{k}\\ & =(v_2\cdot w_3-v_3\cdot w_2)\cdot \vec{i}-(v_1\cdot w_3-v_3\cdot w_1)\cdot \vec{j}+(v_1\cdot w_2-v_2\cdot w_1)\cdot \vec{k}\end{array}$$

Properties §

1. $\vec{v}\times \vec{w}=-\vec{w}\times \vec{v}$ Example:

$$\begin{array}{rl}\vec{v}\times \vec{w}& =<-10,5,0>\\ \vec{w}\times \vec{v}& =<10,-5,0>\end{array}$$

2. $\vec{v}\times \vec{v}=0$ Proof:

$$\begin{array}{rl}& \vec{v}\times \vec{v}=-\vec{v}\times \vec{v}⟹\vec{v}\times \vec{v}=0\end{array}$$

3. $\vec{v}\times (\vec{u}+\vec{w})=\vec{v}\times \vec{u}+\vec{v}\times \vec{u}$
4. For $c\in \mathbb{R}$ we have

$$\begin{array}{r}c\times \vec{v}\times \vec{u}\end{array}$$

Test for Parallel Vectors §

For nonzero vectors $\vec{v}$ and $\vec{w}$ in ${\mathbb{R}}^3$ we say that $\vec{v}$ and $\vec{w}$ are parallel to each other if and only if their dot product is the zero vector. ($\vec{v}\times \vec{w}=\vec{0}$).